Wordle is a pleasant game that is enjoyed by all. To set up some terminology, there is a secret five-letter word (the target) you are trying to guess. You enter your guess (another five-letter word), then receive feedback in the form of a pattern, where the letters in your guess are colored in three different ways:
⬛ Black means the letter is not present in the target word.
🟨 Yellow means the letter is present in the target word, but not in the same position as in the guess.
🟩 Green means the letter is present in the target word, in the same position as in the guess.
A pattern is a sequence of five of these blocks. You have six guesses to identify the target.
I did an information-theoretic analysis on a napkin to find the best initial guess and I thought I’d write it up. So here you go. With some modifications the analysis can give you the optimal guess at each point, too. This forms a nice example of information-theoretic thinking. This post assumes in the main text that you know basic information-theoretic measures, but it explains them in footnotes in case you don’t.
🚨🚨WARNING🚨🚨: For some people, taking an optimization approach makes the game less fun. I do calculate the optimal first guess here, but it’s at the end and hidden behind a link. Consider yourself warned!
The Setting
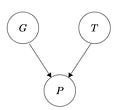
First, we formulate the problem probabilistically. Let T be a random variable with support over vocabulary W, representing the unknown target word. Let G be the random variable representing your guess, also with support over vocabulary W. Finally let P be the random variable over patterns that result from your guess: P is a deterministic function of a guess g and a target t, which we can write as p = f(t, g). The variables are structured like this:
This diagram means that the joint distribution on all three variables factorizes as
This is an interesting pattern of statistical dependence called “explaining away” or “synergy”. It’s interesting because T and G initially are independent of each other (obviously you don’t know the target when you formulate your guess), but if you consider the conditional distribution P(T, G | P), suddenly they become dependent on each other. In terms of information theory we have that the mutual information of T and G is zero1
but the conditional mutual information is nonzero
This means that the tripartite mutual information of T, G, and P will be negative. Similar logic comes up in the information-theoretic analysis of cryptography: considered without the encryption key, a ciphertext has zero information about the underlying plaintext, but if you condition on the encryption key, suddenly the ciphertext gives you all the information about the plaintext. In the case of Wordle, your guess is uninformative about the target until you get the pattern. The pattern is like an encryption key that makes your guess informative about the target.
We can note down further constraints on the variables. Because the pattern is a deterministic function of the target and the guess, we have that the conditional entropy of P given G and T is zero:2
We’ll use these assumptions in the derivation below.
Intuition
Given a guess and pattern, there is a set of possible target words compatible with the guess and the pattern. You want to choose a guess such that this set is small on average across possible targets.3 We’ll see that the information-theoretic solution reflects this intuition directly: you want to find a guess that minimizes the average (logarithm of the) size of the resulting set of compatible words.
In fact, I came up with the intuition above first, and then wrote a Python script to find the best first guess by this logic, and worked out the actual derivation on a napkin while the script was running. It’s nice that grinding out the math gives you such an intuitive conclusion in the end, and I think it gives a glimpse of how information theory works.
Finding the Optimal First Guess
From an information-theoretic perspective, the optimal initial guess is the one which is maximally informative about the target, given the resulting pattern. That is, it is the guess which maximizes the information content about the target, given the resulting pattern. For maximum generality, we seek the optimal guessing policy, a distribution P(g), to maximize the conditional mutual information between the guesses G and targets T given patterns P:
Find P(g) to maximize I[T : P | G].
To analyze this, first we’ll rewrite the mutual information in terms of a difference of conditional entropies:
The trick here is that the first term, H[T | G], is irrelevant to the optimization problem. We can see this by rewriting it like so:
According to the structure of the problem, we have I[T : G] = 0. That is, a guess is not informative about the target in the absence of the resulting pattern. So the conditional entropy H[T | G] is nothing but the entropy of targets H[T], which is not a function of P(g). That means we can forget about it! It’s just a constant as far as we’re concerned. Dropping the term H[T | G] from our optimization objective, we’re left with an equivalent but simpler optimization problem, to wit, we want to minimize the conditional entropy of targets given guesses and patterns:
Find P(g) to minimize H[T | G, P].
So our goal is to find the guess policy that will reduce our uncertainty about the target as much as possible. As the next step, we’ll unpack the conditional entropy:
Now we’ll assume that target variable T has a uniform distribution on the vocabulary. This is a maximum-entropy assumption, that is to say, I am assuming we have maximal uncertainty about the target T.4 The result is that the conditional probability of particular target t given a particular guess g and pattern p is just uniform over the set of possible targets compatible with the guess and pattern:
where I’ve made up the notation W(g, p) to refer to the set of vocabulary words compatible with guess g and pattern p:
So now we’ve whittled the conditional entropy down to
Only a few more steps to go. For the probability of a pattern p given a target t and guess g, that’s easy—the pattern is a deterministic function of the target and the guess. So we can write the probability as an indicator function, which I notate using an Iverson bracket:
This Iverson bracket has value 1 when f(g, t) = p and 0 otherwise. Now under our maximum-entropy assumption about targets T, and re-arranging the sums a little bit, we get
Whenever you see a sum next to an Iverson bracket, you can think of the bracket as filtering the output of the sum. In our case, for each target t and guess g, there is only one pattern p that will not get zeroed out by the Iverson bracket: the actual pattern corresponding to t and g. So we can drop the sum on patterns, and write in the expression for the surviving pattern p directly, to get:
The optimal strategy is now to concentrate all the probability mass in P(g) onto the single guess g that minimizes
That’s it! We want to find the guess that minimizes the average (log) size of the set of targets compatible with the resulting pattern. The step-by-step derivation leads back to the simple intuition above.
But it goes beyond that intuition, because it shows why it is justified, and it also points toward potential better strategies. In particular, if you knew the real distribution P(t) on targets—that is, if you knew how the targets were selected—then you wouldn’t have to assume a uniform distribution like we did, and you could follow the information-theoretic logic to get a provably better first guess. In fact, the real distribution on targets is almost certainly not uniform. To some extent, targets are selected to be interesting, so a good model of P(t) would assign probability to words proportional to their interestingness, whatever that is.
Implementation, and the Answer You’re All Here For
If you have a word list, finding the guess g to maximize informativity can be done with a simple Python script. The only trick is you don’t want to calculate the size of the compatible set |W(g, f(g, t))| over and over again for each target t; just compute it once for each pattern and save the result.
Using the wordlist here, I calculated the single optimal first guess: it is found here. [Edit: Using the real wordlist, which I found thanks to commenter Darley below, the best guess is found here.] The mutual information I[T : P | G] for this guess is 5.5 bits. You’ll get a different solution when you use a different wordlist. If someone knows the wordlist that is actually used in the game, leave a comment in my webzone below.
Other Intuitions
When I first started playing Wordle, my strategy was to try to guess words with high-frequency letters. I found myself trying to work RSTLNE into my guesses, inspired by Wheel of Fortune.
Interestingly the optimal first guess derived above does indeed have many frequent letters in it. But the guess-a-lot-of-high-frequency-letters isn’t optimal in general, for severals reasons. For example, it doesn’t consider the effects of letter position. Nevertheless, it does seem to be a good heuristic, and it would be cool to see a proof that it is an approximately optimal strategy!
Mutual information is the quantity that tells you how many bits of information one random variable provides about another. For random variables X and Y, it is a log probability ratio
where the sum is over all the combinations of values of x from the support of X and y from the support of Y. I use similar sum notation everywhere. When the logarithm is in base 2, you can interpret it as the bits of information provided by X about Y—and vice versa, because it’s symmetrical.
Entropy quantifies the uncertainty present in a random variable, or equivalently, the amount of information in the random variable. It is the average log probability of values of X:
High entropy means high uncertainty; you can relate entropy to the number of guesses that it takes the guess the value of a random variable. Conditional entropy of a random variable X given another random variable Y is the remaining uncertainty about X after taking into account all the information in Y:
For example, we’re going to see that it is useful to find the guess that minimizes the conditional entropy of the target given the guess and the pattern.
Conditional entropy is related to mutual information in some intuitive ways. The conditional entropy of X given Y is just the entropy of X minus the mutual information of X and Y:
That’s just the initial uncertainty about X minus the information provided by Y. And so you can also write the mutual information in terms of conditional entropy, as
It might be more complicated in Hard Mode, when all guesses are constrained to use the letters revealed by previous guesses. In that case your guess not only reduces the set of compatible targets, it also constrains your future guesses. I’m not sure if the same strategy is optimal in that case. So this is officially an analysis of Easy Mode.
We could do better than the analysis here if we knew something about the true distribution on targets P(t). More on this later.


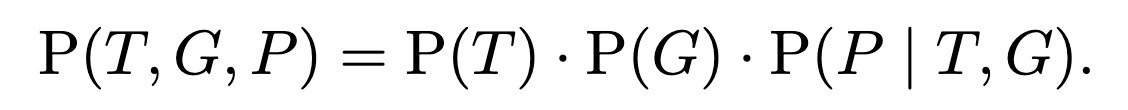
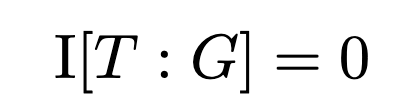
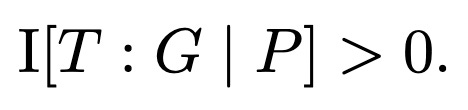
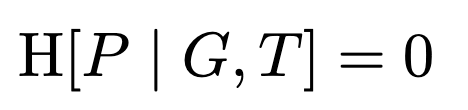
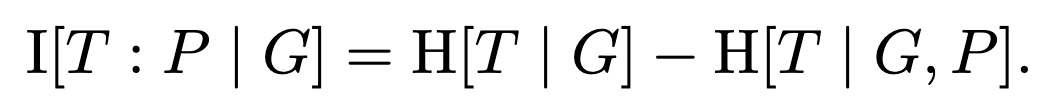
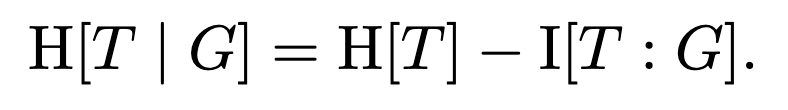
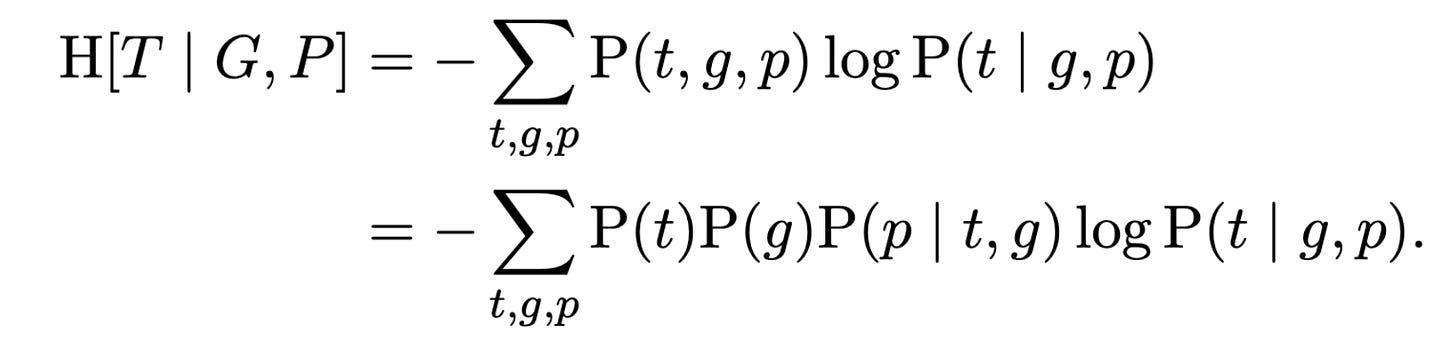
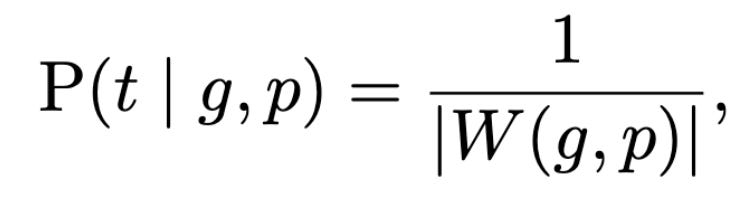
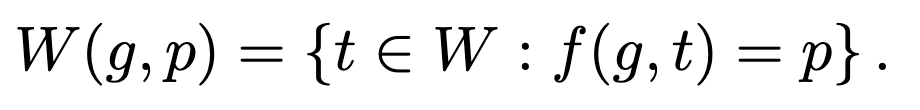

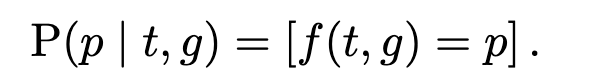
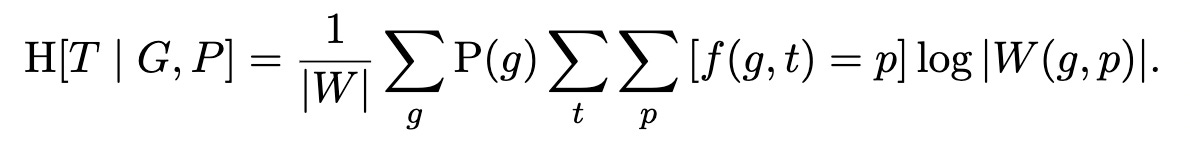
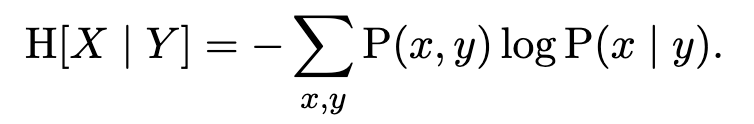
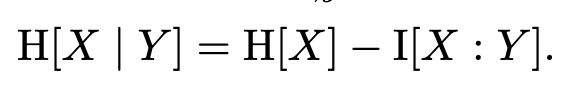
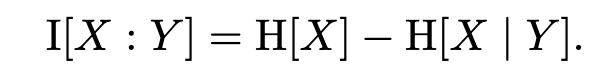
The full word list is available in the code of Wordle, in a long string
In the first paragraph of "Finding the Optimal First Guess", it says: "a distribution P(g), to maximize the conditional mutual information between the guesses G and targets T given patterns P:", but the expression following this sentence, it is showing I(T : P | G), i.e., the mutual information between the patterns P and the targets T given the guess G, which seems more correct. The text should be amended.